[NOIP2002 普及组] 过河卒

题目描述

棋盘上 AA 点有一个过河卒，需要走到目标 BB 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 CC
点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，AA 点 (0,0)(0, 0)、BB 点 (n,m)(n, m)，同样马的位置坐标是需要给出的。

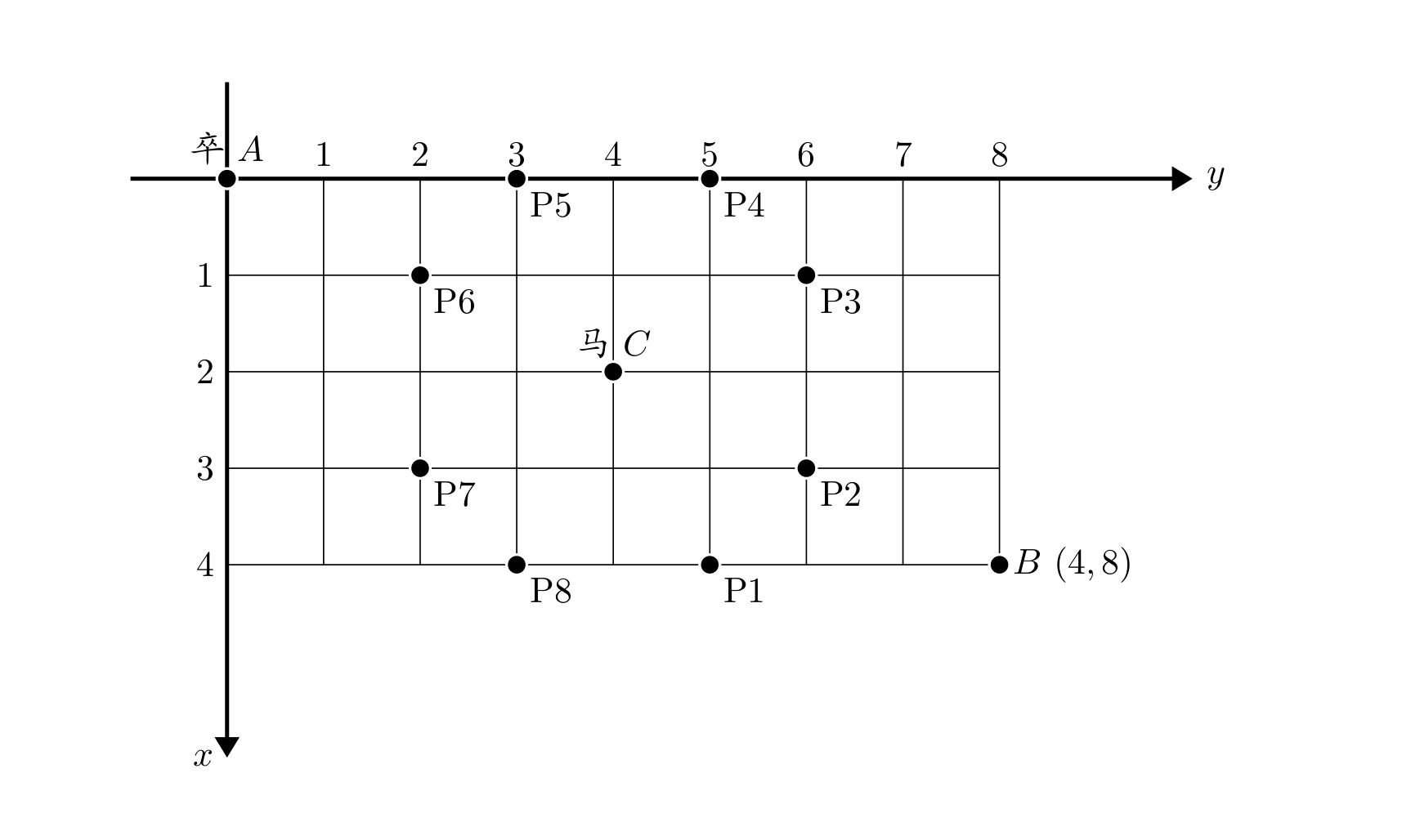
现在要求你计算出卒从 AA 点能够到达 BB 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 BB 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

样例 #1

样例输入 #1

1
6 6 3 3

样例输出 #1

1
6

提示

对于 100%100 \% 的数据，1≤n,m≤201 \le n, m \le 20，0≤0 \le 马的坐标 ≤20\le 20。

【题目来源】

NOIP 2002 普及组第四题

思路

这道题是2002年普及组第四题，所以难度不高，看到这道题，很容易想到是一个动态规划，那就好解了，唯一区别就是额外处理一下马的位置就行，用DP不会超时，如果跟走迷宫一样从(
0,0)走，会超时。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <bits/stdc++.h> //万能头
using namespace std;
typedef long long ll; //后面多次用到long long，为了方便，后面直接写ll
int n, m, house_vis[25][25], h_n, h_m; // n,m为棋盘的参数，house_vis是马可以走到的位置，不能走。h_n和h_m为马的坐标
ll ans;  // 路径个数 开ll
ll f[25][25];  //同样开ll
int house[8][2] = {{2, 1}, {1, 2}, {-1, 2}, {-2, 1}, {-2, -1}, {-1, -2}, {1, -2}, {2, -1}}; //马走日，可以走八种方向，采用打表的方式
bool in_mg(int x, int y) //判断是否可走，主要判断两点，首先是是否在迷宫内部，其次是该坐标是否是马能走到的点（不能走）
{
    return x >= 0 && x <= n && y >= 0 && y <= m && house_vis[x][y]!=1; //返回布尔值
}
ll dfs(int x, int y)  //实现动态规划，开ll
{
    if (!in_mg(x,y)) return 0; //不在迷宫内
    if (x == 0 && y == 0) //倒着走，走到起点了，说明有路，返回1
        return 1;
    if (f[x][y] != -1)  //这个点之前走过了，我们把数组这一项的数据返回
        return f[x][y];
    f[x][y] = dfs(x - 1, y) + dfs(x, y - 1); // 这个点没有走过，计算路径
    return f[x][y];
}
int main()
{
    cin >> n >> m >> h_n >> h_m;
    house_vis[h_n][h_m] = 1; // 马的位置 不能走
    for (int i = 0; i < 25; ++i)
    {
        for (int j = 0; j < 25; ++j)
        {
            f[i][j] = -1; // 路径数组，元素都初始化为 -1
        }
    }
    for (int i = 0; i < 8; i++)
    {
        int No_x = h_n + house[i][0]; // 马可以走到的点x坐标
        int No_y = h_m + house[i][1]; // 马可以走到的点y坐标
        if (in_mg(No_x, No_y))  //判断是否在迷宫内部，防止坐标小于0的情况。。。
            house_vis[No_x][No_y] = 1; // 马能走到的点 不能走
    }
    ans = dfs(n,m);  //计算
    cout<<ans;  //输出
    return 0;
}